你以為不可能，其實只是樣本不夠大：用 Rust 跑 Monte Carlo 爆破低機率

從一支「看起來不可能」的影片開始

前陣子在 YouTube 上滑到一支丁特幾年前的影片，內容是大家很熟悉的那種情境：抽卡、爆裝、成功率極低，但實際結果卻誇張到讓人懷疑人生。

當下我的第一個反應不是羨慕，也不是嘲諷，而是單純卡在一個點上：這個機率，真的低到「不應該發生」嗎？

我們平常看這類影片，常常會用一句話帶過：「這太扯了啦，根本不可能。」

但這句話其實隱含了一個假設：我們的直覺是可靠的。偏偏，機率是最喜歡打臉直覺的東西。

當直覺開始懷疑機率

如果你問我為什麼會真的動手寫程式，而不是只停在「嘴上吐槽」，答案其實很簡單：

因為我發現，我自己也說不清楚「不可能」到底是多不可能。

• 是一百次不會發生一次？
• 還是一萬次？
• 還是只要樣本數夠大，它其實遲早會發生？

我們很習慣用「體感機率」在判斷事情，但這種體感通常只基於：

• 自己的經驗
• 身邊聽過的案例
• 或影片留言區的倖存者偏差

問題是，這些東西加起來，樣本數其實小得可憐。

於是我決定不再用直覺跟直覺吵架，而是換一個方式問問題：

如果我把同一個低機率事件，

重複跑上十萬、百萬次，結果會長什麼樣？

也就是在這個念頭下，我開始動手寫一個簡單的 Monte Carlo 模擬器。

不是為了證明誰歐、誰非，而是想親眼看看：

• 所謂「不可能的事件」
• 在足夠大的樣本裡
• 到底會不會、又會怎麼出現

後面的故事，就全部從這裡展開了。

Draw Rate：一次成功的機率 p

這個參數最直覺，也最容易被誤解。

Draw Rate 就是：每一次嘗試，成功的機率是多少？

不管你是抽卡、強化、掉寶，或任何「成功 / 失敗」的事件，本質上都是一次伯努利試驗。問題通常不在於這個數字，而在於我們常常只盯著它看，卻忽略後面還有兩個更關鍵的維度。

Total Players：一次回合做幾次試驗 n

第二個參數，是一次「實驗」裡會做幾次嘗試。

你可以把它想成：

• 一次抽幾抽
• 同一時間有幾個人都在試
• 或某個事件在一個回合內會被觸發幾次

很多「怎麼可能有人這麼歐」的案例，其實不是因為單次機率高，而是因為同一回合裡試的人（或次數）夠多。當 n 一大，極端結果就不再那麼稀奇。

Rounds：你願意給現實多少樣本量

最後一個參數，也是我們直覺最常忽略的：你到底觀察了多少次？

Rounds 代表的是：同樣的實驗，你願意重複跑幾次？

我們日常看到的案例，rounds 通常非常小：

• 自己玩幾次
• 看幾支影片
• 聽幾個朋友分享

但現實世界的 rounds 往往遠超我們的感知範圍。而只要樣本數一大，下面這些事情就會開始發生：

• 一次很低的機率，重複很多次後，不再那麼低
• 「怎麼可能一直沒中」其實是可以用數學算出來的
• 看起來像 bug 的怪事，反而是統計上的必然結果

也正是因為這三個參數同時存在，我才會決定不再只用感覺討論，而是直接讓電腦去幫我把樣本跑到夠大。接下來，就可以正式進入爆破階段了。

公式解能算平均，但看不到極端值

用公式算，你很快就能得到：

• 期望值是多少
• 分佈大概集中在哪
• 理論上標準差有多大

這些都沒有錯，也很重要。但當你在看那些「看起來不可能」的影片時，你在意的通常不是平均，而是：

• 為什麼有人可以這麼歐？
• 為什麼有人可以這麼非？
• 這種極端情況，到底有多罕見？

而這些問題，用一個平均值是回答不了的。

模擬能回答「現實長什麼樣」

Monte Carlo 的想法其實很暴力，也很直覺：

不跟你吵理論，

我直接把同一件事重複做幾十萬、幾百萬次。每一次模擬，都是一次完整的「現實可能發生的版本」。當你把這些結果全部堆在一起，你看到的就不再是單一答案，而是一整個分佈。

你會很清楚地看到：

• 大多數情況會落在哪
• 分佈的尾巴有多長
• 那些「很扯的結果」到底是在分佈的哪個角落

這種「親眼看到現實長什麼樣」的感覺，是公式給不了的。

爆破比背公式更直覺

我其實沒有想把這篇文章寫成一堂機率課。比起背公式、推導、證明，我更想做的是一件事：

把直覺校正回來。

Monte Carlo 對我來說，就是一種「爆破式理解」：

• 不懂沒關係
• 先看結果
• 再回頭理解為什麼會這樣

當你看到分佈慢慢成形，看到極端值真的會出現，你對「低機率事件」的感覺，會自然跟以前不一樣。而這個轉變，正是我做這個實驗真正想要的效果。

直方圖：成功次數的真實分佈

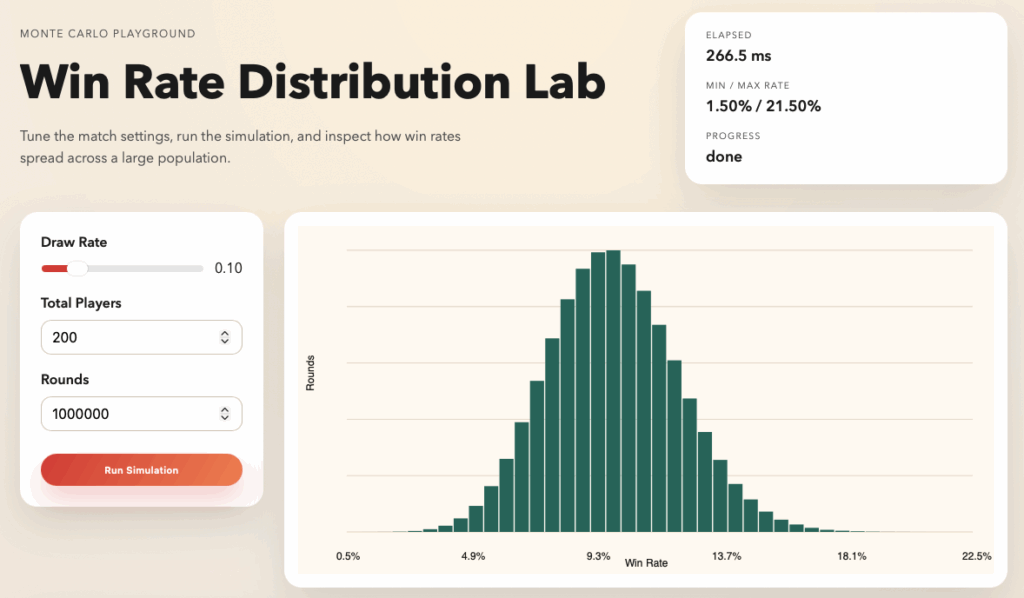
畫面中央最大的那張圖，是一個直方圖。

• x 軸：一次回合裡，成功了幾次（wins）
• y 軸：這個成功次數，在所有 rounds 裡出現了幾次

你可以把它想成是在回答這個問題：

如果我把同樣的低機率事件，重複跑很多次，每一種結果各會出現幾次？

通常你會看到一個很明顯的現象：

大部分結果會集中在中間，長得像一座山。

這座山，就是「現實中最常發生的狀況」。而左右兩側慢慢變細的部分，則是你平常只在影片裡看到的那些極端案例。

表格：每個 win rate 出現了幾次

如果說直方圖是讓你「看感覺」，下面的表格就是讓你「看數字」。

表格會把所有出現過的結果整理成幾個欄位：

• wins：成功次數（或區間）
• win rate：換算成百分比的成功率
• rounds：這個結果出現了幾次
• share：佔所有 rounds 的比例

這張表最有用的地方在於：它會直接告訴你哪些結果是「主流」，哪些只是「尾巴」。

很多時候你會發現：

• 看起來很扯的結果，其實真的存在
• 但它們佔的比例，通常小到你平常根本碰不到

Min / Max Rate：最歐與最非到底能多離譜

最後一個我自己最愛看的指標，在畫面右上角。

Min / Max Rate 代表的是：

• Min Rate：在這次模擬裡，成功率最低的那個回合
• Max Rate：成功率最高的那個回合

換句話說，這兩個數字就是：

「如果你把所有回合排成一排，最非的那個人，跟最歐的那個人，會站在哪裡？」

這個數字通常都會比你心裡預期的還要誇張。也正是看到這裡，你才會真正意識到：

不是世界偏心，而是只要樣本數夠大，極端一定會出現。

接下來，就可以真的把某個「你覺得不可能的機率」丟進去，親眼看它被跑成一整個分佈了。

設定實驗參數

在 Win Rate Distribution Lab 裡，設定實驗其實就是調三個數字：

• Draw Rate：每一次嘗試成功的機率
• Total Players：一個回合裡會做幾次嘗試
• Rounds：整個實驗要重複跑幾次

你可以直接把影片裡提到的成功率丟進來，也可以故意調得更低一點，看看分佈會怎麼變形。

當你按下「Run Simulation」，後端就會開始用 Monte Carlo 的方式，一回合一回合地幫你把結果堆起來。

分佈為什麼會長成一座山

跑到一定數量之後，你幾乎一定會看到同一個畫面：

直方圖開始慢慢長成一座「山」。

這不是巧合，而是因為：

• 大多數回合，結果都會圍繞在某個「最常見區間」
• 偏離這個區間越遠，出現的次數就越少

也就是說，現實其實非常偏好「普通的結果」。你平常玩遊戲、抽卡、強化，大多數時候遇到的，都是這座山中間的那一小段。只是這種結果，通常不會被拍成影片。

極端值什麼時候冒出來

真正有趣的地方，通常發生在你跑得夠久之後。

隨著 rounds 一直增加，你會注意到兩件事：

• 分佈的中間越來越穩定
• 但左右兩側，開始慢慢冒出一些「你不太想看到的數字」

那些就是極端值。

它們出現的頻率很低，低到你平常玩一輩子可能都碰不到一次；但只要你把樣本數撐到夠大，它們就一定會出現。

這也是為什麼很多「看起來超扯」的事件：

• 在單一玩家身上，像奇蹟
• 放到整個世界的樣本裡，只是分佈尾巴的一小點

而這一刻，通常也是直覺開始真正被說服的時候。

為什麼平均值常常騙人

平均值很誠實，但它只回答一個問題：

如果你把所有人的結果攪在一起，平均會長怎樣？

可是在抽卡、爆裝、低機率事件的討論裡，大家真正想問的通常是：

• 為什麼我可以這麼非？
• 為什麼他可以這麼歐？
• 這種差距真的正常嗎？

這些問題，全都跟「尾巴」有關，而不是中間那一大坨。

平均值會把所有極端都沖淡，讓你產生一種錯覺：事情好像沒那麼誇張。

但現實是，分佈從來都不只存在於平均那個點上。

Min Wins：最非的人可以慘到什麼程度

在每一輪模擬裡，我都會去找一個數字：

成功次數最少的那個回合。

這個值通常不會出現在分佈的中間，而是躲在左邊那條細細的尾巴上。

它代表的不是「你會不會遇到」，而是：

如果真的有人站在這條尾巴上，他會慘到什麼程度？

這也是很多人看完模擬後會沉默的地方。因為你會發現，那些你以為「系統一定有問題」的狀況，其實完全落在統計允許的範圍內。

Max Wins：最歐的人為什麼看起來像開掛

另一邊的尾巴，故事就完全不一樣了。分佈右側的極端值，代表的是那個「歐到不行」的回合。成功次數高到你會懷疑是不是忘記算失敗。當你把這個數字拿去跟平均值比，差距往往會大到讓人不舒服。但從統計的角度來看，它並沒有做錯任何事。它只是站在了右邊那條尾巴上。也正是因為這種極端值真的存在，

我們才會一直看到：

• 看起來像神蹟的影片
• 讓人懷疑人生的對比
• 還有永遠吵不完的「機率是不是假的」

而這個模擬要做的，不是替誰平反，而是把這些尾巴，攤開來讓你看清楚。

為什麼不用等全部跑完

如果你一次跑幾十萬、上百萬 rounds，最簡單的做法其實是：

1. 後端全部算完
2. 一次把結果丟回前端
3. 前端畫一張圖

這樣做沒有錯，但有兩個問題：

• 使用者會盯著一個空白畫面，不知道現在在幹嘛
• 你永遠看不到「分佈是怎麼長出來的」

而我更想看到的是：

• 分佈從一團亂開始
• 中間那座山慢慢站穩
• 極端值什麼時候第一次出現

所以我選擇把模擬拆成很多小批次，邊算、邊回傳。

Server-Sent Events（SSE）在做什麼

為了做到這件事，我用了 Server-Sent Events（SSE）。簡單講，它是一種：

伺服器可以主動、不斷往前端「推資料」的方式。

在這個專案裡，後端每跑完一個 batch，就會送出一包資料，裡面包含：

• 目前累積的 counts
• 已完成的進度比例
• 已經花了多久時間
• 當下的最歐與最非

前端不是在「問結果」，而是在「聽直播」。只要連線還在，資料就會一直流過來。

前端如何即時重繪分佈

前端的角色其實很單純。

它只做三件事：

1. 接收 SSE 傳來的新資料
2. 把最新的 counts 畫成直方圖
3. 同步更新表格與指標數字

每次資料一到，畫面就會被重繪一次。你看到的不是動畫，而是真實資料一點一點堆出來的結果。

這種設計帶來的好處是：

• 使用者知道系統正在工作
• 分佈的收斂過程一目了然
• 等待時間本身變成實驗的一部分

對我來說，這比「跑完才給你看」更符合這個實驗的精神。

當 rounds 拉到百萬等級會發生什麼事

一開始我只是想跑個幾萬次看看分佈，大概長這樣：

rounds = 10_000

很快、很舒服、幾乎不用等。但當我開始想看極端值，想看「最非到底能多非」，rounds 就會自然變成：

rounds = 1_000_000

這時候差異就出現了：

• 單次模擬裡有 total_players 次隨機試驗
• 一百萬 rounds 代表的是 數億次 random 判斷
• 再加上還要即時更新分佈

如果後端撐不住，整個實驗體驗就會直接垮掉。

Rust：穩定爆破大量樣本

Rust 版的核心模擬邏輯其實非常樸實，重點只有一個：穩定、可預期、跑得動。

以下是 Rust 版簡化後的核心模擬程式碼（你可以直接拿去玩）：

fn run_simulation(draw_rate: f64, total_players: u32, rounds: u32) -> Vec<u32> {
    let mut counts = vec![0u32; (total_players + 1) as usize];
    let mut rng = rand::rngs::SmallRng::from_os_rng();

    for _ in 0..rounds {
        let mut wins = 0u32;
        for _ in 0..total_players {
            if rng.random_bool(draw_rate) {
                wins += 1;
            }
        }
        counts[wins as usize] += 1;
    }

    counts
}

在實際專案裡，我還多做了幾件事：

• 使用 SmallRng，減少隨機數生成的成本
• 把模擬丟進 spawn_blocking，避免卡住 async runtime
• 拆 batch，用 SSE 把結果一段一段推給前端

這樣的好處是：

• rounds 再大，也只是「多跑一點時間」
• 不會突然卡死或拖垮整個服務
• 行為非常可預期，適合做這種爆破型實驗

Python：可讀性與快速驗證

但話說回來，我還是很喜歡 Python。因為當你只是想確認「概念對不對」，Python 真的寫起來又快又直覺。

下面是 Python 版對應的模擬邏輯：

import random

def run_simulation(draw_rate, total_players, rounds):
    counts = [0] * (total_players + 1)

    for _ in range(rounds):
        wins = 0
        for _ in range(total_players):
            if random.random() < draw_rate:
                wins += 1
        counts[wins] += 1

    return counts

你可以很清楚地看到：

• 每一行幾乎都在對應模型本身
• 不需要理解太多背景就能改參數、加 print
• 非常適合拿來做「小規模試跑」

所以我的實際策略是：

• Python：拿來驗證想法、調模型、快速實驗
• Rust：拿來長時間跑、大樣本爆破、實際部署

如果你只是想在本機玩玩看，甚至可以直接把上面的 Python 程式貼進去跑，把 rounds 往上加，親眼看看分佈怎麼變。

接下來，就可以聊聊我怎麼把它包成跨平台版本，順便丟到線上給大家一起玩了。

Apple Silicon / Windows / Ubuntu 發佈版

我有把 Rust 版整理成三個平台的發佈版本：

• Apple Silicon（macOS / arm64）：點我下載
• Windows（x86_64）：點我下載
• Ubuntu（x86_64）：點我下載

Mac上如果無法執行，請開啟終端機並執行以下指令
xattr -d com.apple.quarantine /path/to/win_rate_distribution && chmod +x /path/to/win_rate_distribution

這裡我會放上兩個檔案，讓你可以自己動手玩：

• main.rs：後端與模擬邏輯的全部入口 點我下載
• Cargo.toml：相依套件與編譯設定 點我下載

如果你想快速理解程式在幹嘛，可以用這個順序看：

1. main.rs 的 router 設定
   • /、/styles.css、/app.js：前端畫面
   • /api/simulate：一次性模擬
   • /api/simulate/stream：SSE 串流模擬
2. 模擬核心邏輯
   • 用隨機數跑大量 rounds
   • 累積每個 wins 出現的次數
   • 不斷回傳目前的分佈狀態
3. 非同步 + blocking 的分工
   • Web server 維持回應
   • 模擬丟給 blocking task 跑
   • 兩邊互不影響

整體設計的目標只有一個：跑得久、跑得大，但服務不會卡住。

HTTPS、自簽憑證與本機測試

為了讓前端的 SSE 在瀏覽器裡行為一致，本機測試時我直接選擇用 HTTPS 跑整個服務。

這裡用的是：

• 自簽憑證（self-signed certificate）
• 啟動時會自動簽署憑證

所以如果你在本機打開時看到瀏覽器警告「不安全」，那是正常的，因為這張憑證本來就不是給公開 CA 簽的。重點不是安全性本身，而是：

• 瀏覽器行為跟線上環境一致
• SSE、EventSource 不會因為 protocol 不同出現奇怪問題

線上試玩

如果你只是想體驗，不想自己跑環境，我也把整個專案部署成線上版本：

👉 https://wr.alfred.wiki

你可以直接在瀏覽器裡：

• 調參數
• 跑模擬
• 看分佈怎麼長出來

而如果你想再多玩一點、甚至改點東西，就可以回頭下載原始碼，自己當一次 cv 工程師。下一段，會聊聊我自己最推薦的幾種玩法，以及哪些參數組合最容易「跑出戲」。

固定成功率，增加 rounds 看分佈如何收斂

第一個玩法最單純，也最適合當起手式。

• 固定一個成功率（draw rate）
• 固定一次回合的試驗次數（total players）
• 只調整 rounds，例如：
  • 10,000
  • 100,000
  • 1,000,000

你會很清楚地看到一件事：rounds 越大，分佈越穩定。一開始直方圖可能長得歪歪的，但隨著樣本數增加，中間那座山會越來越清楚，左右的比例也會慢慢趨於固定。這個過程其實就是在用眼睛看「大數法則」發生。不是用公式證明，而是看它真的長出來。

固定成功率，增加試驗次數觀察極端值

第二個玩法，是我覺得最容易讓人「啊了一聲」的。

• 固定 draw rate
• 固定 rounds
• 慢慢把 total players 往上加

你會發現一個有點反直覺的現象：試驗次數越多，最歐與最非的差距反而越容易被拉開。不是因為成功率變了，而是因為你一次回合裡，給了更多機會讓極端值發生。這也是為什麼在「很多人同時在抽／同時在試」的情境下，總會有人看起來歐到不合理。不是系統偏心，而是樣本在同一回合內被放大了。

調低成功率，體感「不可能」其實只是分佈尾巴

最後一個玩法，專門用來對付那句話：

「這個機率也太低了吧，根本不可能。」

做法很簡單：

• 把 draw rate 往下拉
• 保持足夠大的 rounds
• 看完整個分佈長什麼樣

你會看到：

• 中間那座山整體往左移
• 大部分結果都變得「很慘」
• 但右邊那條尾巴，依然存在

那些尾巴上的點，就是你平常只在傳說或影片裡看到的案例。這個玩法最有趣的地方在於：

它會讓你意識到，「不可能」很多時候只是：你沒有看到那條尾巴而已。

如果你願意把樣本數拉到夠大，現實會比你想像的還誠實，也還殘酷。

你看到的只是分佈的一小塊

透過 Monte Carlo 模擬，我們可以很清楚地看到完整的分佈：

• 大多數結果集中在中間
• 左右兩側的尾巴很細，但確實存在
• 越多樣本，尾巴越容易被看見

但在現實生活中，大多數人看到的，從來都不是這張完整的分佈圖。

我們看到的往往只是：

• 一次歐到不可思議的成功案例
• 或一次非到懷疑人生的個人經驗

這些都是真實發生過的事情，但它們只佔了分佈中的極小一部分。把這些片段拿來代表整個現實，本身就是一種錯誤的理解方式。

現實不偏心，只是樣本夠大

從統計角度來看，現實世界並沒有偏心任何人。

如果同一個低機率事件，被大量重複執行，那麼：

• 有人會站在左邊的尾巴
• 也一定會有人站在右邊的尾巴

這些人不是比較衰，也不是比較幸運，而是剛好站在了分佈的不同位置。

真正的問題在於：

大多數人並不知道這張分佈長什麼樣。

當你只看到中間或某一側的結果時，很容易產生錯誤的期待，甚至錯誤的判斷。

當「可能發生」變成行銷語言

從統計角度來說，「可能發生」通常是一句沒有錯的話。問題在於：它太容易被拿來當作行銷話術的護身符。

因為「可能」的語意非常滑。它同時可以代表：

• 幾乎每個人都碰得到（例如 20%）
• 也可以代表你一輩子都未必遇到一次（例如 0.01%）

但宣傳文案很少會把「可能」背後的量級說清楚。於是玩家看到的就變成一種非常典型的資訊落差：

1. 宣傳把鏡頭對準分佈的尾巴社群貼文、廣告素材、直播精華、短影音——最適合被拿來傳播的永遠是「有人抽到」、「一發入魂」、「超歐瞬間」。這些都是真實事件，但它們在整體分佈裡通常是非常細的尾巴。把尾巴當主菜，玩家自然會誤判整體長相。
2. 把「個案」包裝成「你也可以」很多行銷不會明講「你一定抽得到」，但會用暗示式敘事：「只要參與就有機會」、「下一個就是你」、「祝你一發畢業」。這些句子不構成保證，卻會讓消費者在心理上把自己往分佈右側靠攏——而且越在情緒高點越容易發生。
3. 用『隨機』掩蓋『資訊缺席』「一切都是隨機」本身是描述機制，不是解釋體驗。如果你不提供合理的量化資訊（例如機率、期望成本、分佈區間），那玩家無從判斷自己到底是在跟什麼規模的風險互動。這時候「隨機」就會變成一個很方便的結語：講完就收，拒絕溝通。
4. 把玩家的直覺缺口變成變現空間抽卡機制的商業強度，很大一部分是建立在「人類不擅長直覺理解低機率」這件事上。當業者知道玩家會高估自己成為歐皇的機率、低估落入尾巴左側的成本時，宣傳只要一直把歐的片段推到你面前，玩家就會更難冷靜評估。

所以我覺得關鍵不是「極端值能不能發生」——它當然能。

真正該被檢視的是：業者是否用『可能發生』這句真話，去包裝一個讓人誤判風險的溝通方式。

統計上成立，不代表宣傳上合理。

尤其當它直接牽涉到付費決策時，這就不是單純的「大家都知道機率很低」可以帶過的問題。

扭蛋法與機率揭露：制度試圖補上的那一塊

如果把抽卡/轉蛋機制當成一種「機率型商品」，那制度要處理的核心其實很清楚：資訊不對稱。

玩家社群這幾年的討論，很多時候不是在追求「公平到大家都抽得到」，而是在問一個更基本的問題：

我付錢之前，能不能知道我到底買的是什麼風險？

因為在一般消費市場裡，商品資訊揭露是基本原則：

你買一台電器要看規格、買食品要看成分、買保險要看條款。

但在機率型虛擬商品裡，玩家往往只拿得到「很抽象的描述」，例如：

• 機率很低／機率不高
• 有機會獲得
• 稀有道具限時登場

這些描述在法律或公關層面可能很安全，但在消費者理解上幾乎沒有幫助。

於是制度討論（不管叫不叫扭蛋法）真正想補的，是讓資訊至少達到可被理解、可被比較、可被驗證的程度。

我認為「機率揭露」最低限度可以包含幾個層次（由淺到深）：

1. 單次機率的透明最基本的：每一個獎項或每一個稀有度到底是多少機率。至少讓玩家知道 1%、0.1%、0.01% 是不同世界。
2. 不同條件下的機率變化很多機制會有「活動加成、階段式池子、保底、分段權重、抽到某物後機率調整」等設計。如果只揭露一個靜態百分比，而實際上機率會隨狀態改變，那玩家拿到的仍然不是完整資訊。
3. 期望成本與分佈的概念（不是只給平均）只公布單次機率還不夠，因為玩家真正的問題是：「我大概要花多少？」但平均值又很容易誤導（因為尾巴很長）。更好的揭露方式應該讓玩家理解「常見區間」與「尾巴風險」：例如「抽到目標在 50% 的玩家需要多少抽」、「90% 的玩家需要多少抽」之類的分位數資訊（或等價呈現）。
4. 可驗證性：玩家如何知道它真的照這個機率跑這是最敏感也最重要的一層。如果機率揭露只是公告，但玩家無法用任何方式驗證「公告 ≈ 實際」，那就會永遠停留在信任問題。制度之所以被討論，很多時候正是因為市場機制缺乏可驗證性，導致「信者恆信、不信者恆不信」。

而我覺得制度討論最值得被看見的地方是：

它不是要把遊戲變成慈善，也不是要阻止業者做營收，而是把抽卡這件事從「情緒購買」拉回「資訊充分的決策」。當玩家能更清楚地看到分佈、看到尾巴、知道自己可能站在哪裡，才有可能在理解風險的前提下選擇參與——或者選擇不參與。

這不是在破壞遊戲，而是在把消費行為拉回它本來就應該有的樣子：

你知道你在買什麼，然後再決定要不要買。

工具與模擬能做的，不是替誰背書

我做這個 Win Rate Distribution Lab，從來不是為了替任何遊戲公司辯護，也不是要說「抽不到很正常，你應該接受」。

這個工具真正想做的只有一件事：

把模糊的「可能」，攤成一張你看得懂的分佈。

當你看到整張圖，而不只是其中一個故事時，你對低機率事件的理解會自然變得不一樣。你不一定會比較開心，但你會比較清楚。

如果你也有想爆破的機率情境

如果你還有其他想驗證的情境——不管是抽卡、爆裝、掉寶率、勝率、連敗，甚至保底機制——都可以把它丟進模型裡跑跑看。

理解分佈、理解尾巴、理解自己可能站的位置，永遠比一句「這不可能」來得更有力量。

至少，你是在看清現實之後，再決定要不要跳進去。

後端模擬流程

後端的核心任務其實很單純：

大量重複同一個低機率實驗，並且穩定地把中間結果送出去。

整個流程可以概括成五個步驟：

1. 接收參數
   • draw rate（單次成功機率）
   • total players（一次回合的試驗次數）
   • rounds（要跑幾回合）
2. 初始化統計結構
   • 建立一個 counts 陣列
   • index 代表成功次數（wins），value 代表出現次數
3. 進入大量迴圈
   • 每一回合模擬 total_players 次隨機試驗
   • 計算該回合的 wins
   • 對應的 counts[wins] += 1
4. 批次化執行（batch）
   • 不一次跑完所有 rounds
   • 每跑完一小批，就整理一次目前的分佈狀態
5. 回傳中間結果
   • 計算目前的 min / max wins
   • 計算進度與耗時
   • 將 snapshot 丟給前端

這樣的設計讓後端可以：

• 長時間跑大量樣本
• 同時保持服務可回應
• 不會因為一次大計算而整個卡死

Stream payload 設計

後端每次透過 SSE 推送的資料，都是一包「當下狀態快照」，而不是最終結果。

payload 的設計重點只有一個：

前端收到這包資料，就能直接重畫畫面，不需要再補任何資訊。

概念上包含以下欄位：

• counts：目前累積的成功次數分佈
• progress：完成進度（0～1）
• elapsed_ms：目前已耗時多久
• total_players / total_rounds：實驗參數
• min_wins / max_wins：目前觀察到的極端值
• done：是否已完成全部 rounds

這樣的好處是：

• 前端是「無狀態的」
• 不需要記住歷史，只需要相信最新一包資料
• SSE 斷線重連或中途停止都很乾淨

前端 Canvas 與互動細節

前端的角色非常克制：

不算機率、不推理，只負責畫。

主要分成三件事：

1. Canvas 繪圖
   • 把 counts 當成直方圖資料
   • 動態計算 bar width、高度比例
   • 自動根據 min / max wins 調整可視範圍
2. 互動處理
   • 滑鼠 hover 時，反算目前指到的是哪個 wins
   • 高亮對應的 bar
   • 同步標示下方表格的列
3. 狀態同步
   • SSE 每來一包資料就重繪一次
   • 視窗 resize 時重新計算比例
   • 模擬完成後自動解除鎖定按鈕

整個前端刻意不依賴任何大型圖表套件，我希望它的行為是完全可控、沒有黑盒子的。